what are sets?

In mathematics, a set is a well-defined collection of distinct elements or members. The elements that make up a set can be anything: people, letters of the alphabet, or mathematical objects, such as numbers, points in space, lines or other geometrical shapes, algebraic constants and variables, or other sets. Two sets are equal if and only if they have precisely the same elements.

What is the operation of two sets?

Basic operations

There are several fundamental operations for constructing new sets from given sets.

Unions

The union of A and B, denoted A ∪ B

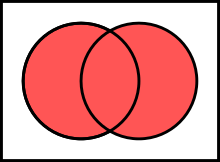
Two sets can be "added" together. The union of A and B, denoted by A ∪ B, is the set of all things that are members of either A or B.

Examples:

  • {1, 2} ∪ {1, 2} = {1, 2}.
  • {1, 2} ∪ {2, 3} = {1, 2, 3}.
  • {1, 2, 3} ∪ {3, 4, 5} = {1, 2, 3, 4, 5}

Some basic properties of unions:

  • A ∪ B = B ∪ A.
  • A ∪ (B ∪ C) = (A ∪ B) ∪ C.
  • A ⊆ (A ∪ B).
  • A ∪ A = A.
  • A ∪ ∅ = A.
  • A ⊆ B if and only if A ∪ B = B.

Intersections


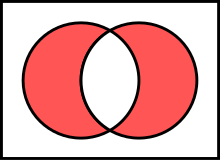
A new set can also be constructed by determining which members two sets have "in common". The intersection of A and B, denoted by A ∩ B, is the set of all things that are members of both A and B. If A ∩ B = ∅, then A and B are said to be disjoint.

The intersection of A and B, denoted A ∩ B.

Examples:

  • {1, 2} ∩ {1, 2} = {1, 2}.
  • {1, 2} ∩ {2, 3} = {2}.
  • {1, 2} ∩ {3, 4} = ∅.

Some basic properties of intersections:

  • A ∩ B = B ∩ A.
  • A ∩ (B ∩ C) = (A ∩ B) ∩ C.
  • A ∩ B ⊆ A.
  • A ∩ A = A.
  • A ∩ ∅ = ∅.
  • A ⊆ B if and only if A ∩ B = A.

Complements

The relative complement
of B in A
The complement of A in U
The symmetric difference between A and B

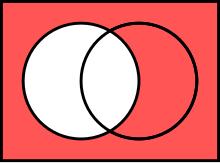
Two sets can also be "subtracted". The relative complement of B in A (also called the set-theoretic difference of A and B), denoted by A \ B (or A − B), is the set of all elements that are members of A, but not members of B. It is valid to "subtract" members of a set that are not in the set, such as removing the element green from the set {1, 2, 3}; doing so will not affect the elements in the set.

In certain settings, all sets under discussion are considered to be subsets of a given universal set U. In such cases, U \ A is called the absolute complement or simply complement of A, and is denoted by A′ or Ac.

  • A′ = U \ A

Examples:

  • {1, 2} \ {1, 2} = ∅.
  • {1, 2, 3, 4} \ {1, 3} = {2, 4}.
  • If U is the set of integers, E is the set of even integers, and O is the set of odd integers, then U \ E = E′ = O.

Some basic properties of complements include the following:

  • A \ B ≠ B \ A for A ≠ B.
  • A ∪ A′ = U.
  • A ∩ A′ = ∅.
  • (A′)′ = A.
  • ∅ \ A = ∅.
  • A \ ∅ = A.
  • A \ A = ∅.
  • A \ U = ∅.
  • A \ A′ = A and A′ \ A = A′.
  • U′ = ∅ and ∅′ = U.
  • A \ B = A ∩ B′.
  • if A ⊆ B then A \ B = ∅.

An extension of the complement is the symmetric difference, defined for sets A, B as

For example, the symmetric difference of {7, 8, 9, 10} and {9, 10, 11, 12} is the set {7, 8, 11, 12}. The power set of any set becomes a Boolean ring with an asymmetric difference as the addition of the ring (with the empty set as a neutral element) and intersection as the multiplication of the ring.

Cartesian product


A new set can be constructed by associating every element of one set with every element of another set. The Cartesian product of two sets A and B, denoted by A × B, is the set of all ordered pairs (a, b) such that a is a member of A and b is a member of B.

Examples:

  • {1, 2} × {red, white, green} = {(1, red), (1, white), (1, green), (2, red), (2, white), (2, green)}.
  • {1, 2} × {1, 2} = {(1, 1), (1, 2), (2, 1), (2, 2)}.
  • {a, b, c} × {d, e, f} = {(a, d), (a, e), (a, f), (b, d), (b, e), (b, f), (c, d), (c, e), (c, f)}.

Some basic properties of Cartesian products:

  • A × ∅ = ∅.
  • A × (B ∪ C) = (A × B) ∪ (A × C).
  • (A ∪ B) × C = (A × C) ∪ (B × C).

Let A and B be finite sets; then the cardinality of the Cartesian product is the product of the cardinalities:

  • | A × B | = | B × A | = | A | × | B |.

what is the membership of sets?

Membership

If B is a set and x is one of the objects of B, this is denoted as x ∈ B, and is read as "x is an element of B", as "x belongs to B", or "x is in B". If y is not a member of B then this is written as y ∉ B, read as "y is not an element of B", or "y is not in B".

For example, with respect to the sets A = {1, 2, 3, 4}, B = {blue, white, red}, and F = {n | n is an integer, and 0 ≤ n ≤ 19},

4 ∈ A and 12 ∈ F; and
20 ∉ F and green ∉ B.

Subsets:

If every element of set A is also in B, then A is said to be a subset of B, written A ⊆ B (pronounced A is contained in B). Equivalently, one can write B ⊇ A, read as B is a superset of A, B includes A, or B contains A. The relationship between sets established by ⊆ is called inclusion or containment. Two sets are equal if they contain each other: A ⊆ B and B ⊆ A is equivalent to A = B.

If A is a subset of B, but not equal to B, then A is called a proper subset of B, written A ⊊ B, or simply A ⊂ B (A is a proper subset of B), or B ⊋ A (B is a proper superset of A, B ⊃ A).

The expressions A ⊂ B and B ⊃ A are used differently by different authors; some authors use them to mean the same as A ⊆ B (respectively B ⊇ A), whereas others use them to mean the same as A ⊊ B (respectively B ⊋ A).

Examples:

  • The set of all humans is a proper subset of the set of all mammals.
  • {1, 3} ⊂ {1, 2, 3, 4}.
  • {1, 2, 3, 4} ⊆ {1, 2, 3, 4}.

There is a unique set with no members, called the empty set (or the null set), which is denoted by the symbol ∅ or {} (other notations are used; see empty set). The empty set is a subset of every set, and every set is a subset of itself:

  • ∅ ⊆ A.
  • A ⊆ A.
Euler and Venn diagrams:

An Euler diagram is a graphical representation of a set as a closed-loop, enclosing its elements, or the relationships between different sets, as closed loops. If two sets have no members in common, the loops do not overlap.

This is distinct from a Venn diagram, which shows all possible relations between two or more sets, with each loop overlapping the others.

Partitions:

A partition of a set S is a set of nonempty subsets of S, such that every element x in S is in exactly one of these subsets. That is, the subsets are pairwise disjoint (meaning any two sets of the partition contain no element in common), and the union of all the subsets of the partition is S.

Power sets:

The power set of a set S is the set of all subsets of S. The power set contains S itself and the empty set because these are both subsets of S. For example, the power set of the set {1, 2, 3} is {{1, 2, 3}, {1, 2}, {1, 3}, {2, 3}, {1}, {2}, {3}, ∅}. The power set of a set S is usually written as P(S).

The power set of a finite set with n elements has 2n elements. For example, the set {1, 2, 3} contains three elements, and the power set shown above contains 23 = 8 elements.

The power set of an infinite (either countable or uncountable) set is always uncountable. Moreover, the power set of a set is always strictly "bigger" than the original set, in the sense that there is no way to pair every element of S with exactly one element of P(S). (There is never an onto map or surjection from S onto P(S).

De Morgan's laws

Augustus De Morgan stated two laws about sets.

If A and B are any two sets then,

  • (A ∪ B)′ = A′ ∩ B′

The complement of A union B equals the complement of A intersected with the complement of B.

  • (A ∩ B)′ = A′ ∪ B′

The complement of A intersected with B is equal to the complement of A union to the complement of B.


Karachi SSC I & II Math Lecture | Chapter 01 | Sets | by sir shahzaib